If I had an opportunity to take a university course now (though it'd be considered late in life at my age), it'd definitely be related to mathematics.
Math is just so damn cool and rewarding. I can't believe it's not emphasized more in the educational curriculum, being so practical. There's a lot of rather basic math which is incredibly useful in everyday life. Of course as a software engineer I might be biased towards overestimating its usefulness due to using it at work and I'm definitely biased towards branches of maths I know and use, which of course is a very limited subset of all math. In the past few years I've found the following pieces/branches of math very useful:
-
Some people cannot multiply exponents with the same bases, even though it's pretty basic math. Even within my own community of software engineers and even when limiting the base to 2 (which is the most common base in computer science) some people have the “deer-in-the-headlights” look when asked to calculate, say, \(2^{13}\), without realizing it is the same as a much more accessible and solvable \(2^{10} \cdot 2^3 = ~1000 \cdot 8 = ~8,000\). Learning rules of exponents gives you great bang for the buck as it can be used in many techniques, such as approximating (which I'll talk about further below). Even if you have different bases, you can make them roughly same by rounding (which will introduce some error). For example if you need to multiply \(10^3 \cdot 3^5\), you may realize that 10 is close enough to \(3^2\) (which is 9) and you can replace 10 with it so that the multiplication becomes \((3^2)^3 \cdot 3^5 = 3^6 \cdot 3^5 = 3^{11} = 177,147\). Exact calculation would yield 243,000, so it's quite a way off but still the right order of magnitude. This technique may come in handy when you're trying to calculate large numbers (at least larger than what those in the primary school multiplication table) - convert them to exponents with the same base and then simply add the exponents. For example, \(150 \cdot 85\) might be approximated as \(2^7 (150 ~= 128) \cdot 2^7\) (also 128, picking a larger value to compensate for the previous smaller number) \(= 2^{14}\). Exact result is 12,750 and the approximation is 16,384 so only overshot by less than 30%. I'm sure there are more precise and more formal ways of approaching this but it can work for rough approximations.
-
This is such an important branch of maths and yet I don't remember any emphasis on it throughout my education and had to re-learn it from scratch as an adult. It's all about counting how many ways there are for something to occur or exist. Many probability problems can be solved with just a combinatorial approach as one of the definitions of probability is the ratio of the number of events we're interested in to the number of all possible events. Counting both of these numbers can quite often be done with combinatorial formulas. An example problem might be: what is the probability that a randomly generated 5-letter password starts with the string “pas” (let's assume passwords are lowercase)? Well, there are 26 letters in the alphabet, so there number of all possible passwords is \(26^5\). The number of passwords that start with “pas” is \(26^2\) (there are only 2 letters to fill) , so the probability is \(\frac{26^2}{26^5} = \frac{1}{26^3}\), or 0.005%. To give a real life example, I used combinatorics to calculate how many unique 3-character passwords might be generated from my bank's code card (and learnt that I will never have to ask for a replacement card during my lifetime, so huge was the number).
-
Probability
Especially binomial coefficients and binomial distribution which are stemming from the idea of Bernoulli trials
-
Statistics
Understanding of basic stats such as measures of centrality (arithmetic average or mean, median), percentiles, probability distributions, etc.
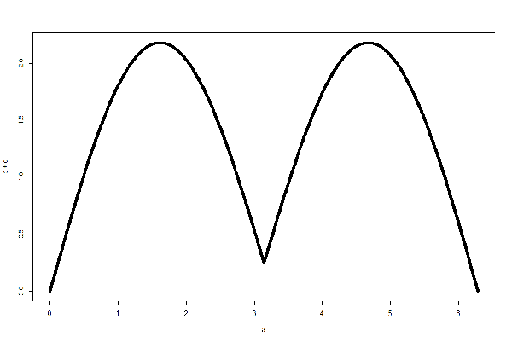
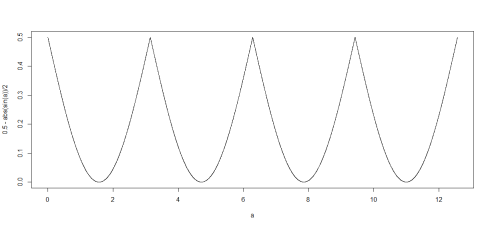
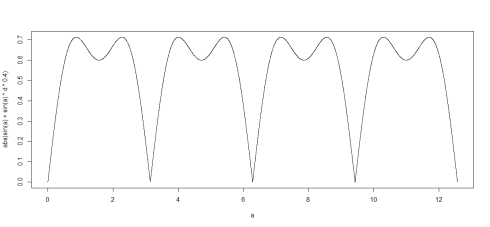
Playing around with graphs of functions is a very entertaining way of learning math, you get to create some spectacular graphs by tweaking and modifying functions and plotting the results. This way you can sort of viscerally learn about behaviour of trigonometric and other types of functions (I mostly played with trig functions as they're periodic). Here are a faux McDonald's logo I created while messing around with functions graphs:
-
While not a perfect imitation, it does resemble the “Golden Arches” of McDonald's. It was made with very simple manipulations of the sine function. The input (X-axis) to the function is some points from 0 to 2π so that we get a single period of the sine function. Then the two “hills” (some argued that they were meant to invoke the image of motherly breasts, but it's a bit of a stretch for me) are made by using the absolute value of sine, so whatever is below 0 on Y-axis gets “rotated around” to be above the Y-axis. Then, to move the sharp cusp that join the arches up a bit, we add a flattened and spread out version of sine wave, with \(\frac{1}{8}\)th of the amplitude and twice the period of the original sine function, so that it has its peak at the joint, i.e. \(y = \frac{sin(\frac{x}{2})}{8}\). The final graph is made by adding those two functions together, \(y = sin(x) + \frac{sin(\frac{x}{2})}{8}\).
Here are some more graphs I created in 30 minutes of playing with graphing software:
-
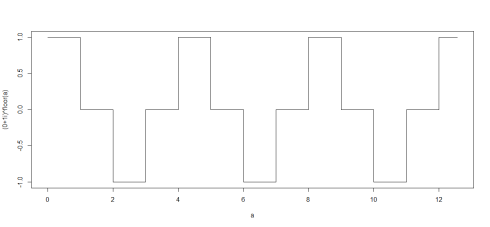
Obstacle course (used imaginary unit to alternate between 1, 0 and -1)
-
Fishy
-
Step-down
-
Step-up
-
Getting louder (slow ramp-up)
-
Getting quieter (fast drop-off)
-
Peaky
-
Molars
-
Grassy hills
-
Overgrown hills (actually same base frequency as the previous graph which kinda still shows through + lots of noise)
-
Noise (normal distribution)
The point is not to create a specific graph but to play around, get the feel for the numbers and learn how to manipulate functions to achieve some effect. Nothing particularly scientific but lots of fun nonetheless!
All these math skills I listed above are useful and interesting but in everyday life other skills that are even more applicable are approximation and estimation.
Approximation
Approximation is unfortunately not really taught in schools. It requires that you don't fixate on getting the absolutely correct (in a precise mathematical sense) answer which may be hard to obtain or actually meaningless (e.g. due to inherent errors in physical measurements) but instead simplify the calculations and get a rough but still good enough answer. We unconsciously do it every day in non-mathematical contexts but often freeze and give up when asked a question that sounds like it requires an exact answer, even though an approximate answer would often do.
Similarly to the example with exponents above, if I get asked how much is \(2^{20}\), I would say it's roughly a million (\(2^{10} \cdot 2^{10} = \sim1,000 \cdot \sim1,000 = 1,000,000\) (or equivalently \(\sim10^3 \cdot \sim10^3 = 10^6\)), unless I need to know exactly how much it is in which case I'd use software to calculate it, I would never think of doing it by hand anymore these days.
It usually doesn't take me more than 2-3 seconds to know answer to base 2 exponentiation problems, because I know the rules of exponents and I know the values of powers of 2 up to the tenth power.
In a way, this means that a lot of math skills I was taught at primary school such as long multiplication or division are no longer useful in today's world where you have powerful software all around you at all times (e.g. your smartphone). I think it would be time much better spent if kids get taught about approximation techniques than slavishly perfect manual calculation algorithms which can be handed off to computers. Spend more time explaining rounding, rules of exponents and logarithms to kids and they'll be much better off in life.
Estimation
Estimation involves approximation but they're not the same. The way I understand estimation is it's a skill that lets you calculate an unknown quantity by first decomposing it into other, more familiar quantities and then building it up again from those better known numbers.
Classic examples include estimating how many ping-pong balls can fit into your living room or the weight of a plane.
Recently (out of boredom) I calculated how long it'll take me to get from the top to the bottom of the mountain on a chairlift. As I was waiting idly with friends at the mountain-top restaurant, I counted the number of chairs in the whole chairlift, that I could see through the restaurant window. Fortunately for me, they were all numbered and 107 was the highest number. So the length of the chairlift was half of that (same number of chairs coming up as coming down) at 54 chairs. Then I counted (in my head only without a watch, like 1.., 2…, 3… and so on) how many seconds passed between each chair. It was roughly 10 seconds. So my rough estimate was 54 \(\cdot\) 10 secs = 540 seconds or 9 mins. The actual ride took 11 minutes but the lift stopped a few times on our way down so my estimate was pretty close.
You may think it's pretty useless to do exercises like that, but I think the more you play with numbers and build your skills and intuition, the easier it gets and the more often you'll apply those skills in your life.
Calibration
To hone those skills I often calibrate my estimates. For example, on my walk to work I know how long it takes me to walk between certain “milestones” (such as intersections or buildings) as I timed it a few times when I first started walking there. In my bathroom there's a tiny toothbrush clock which I normally use for timing of brushing teeth (it came with the toothbrush) but I've also used it to time my showers so I know how long they take (13-15 min, longer if I wash my hair), how long my shaving takes, etc.
Those numbers allow me to be more realistic when planning my schedule for the day. Also since I'm calibrated I can more accurately estimate duration of other activities.
I also calibrate myself on the prices of things, by tracking our spending and knowing how much we spend for food, entertainment or travel per month or yearly. I've developed a good feel for the prices of groceries, simply by paying attention to them so I know what is and what is not the right price for a grocery item. This has positive consequences for my wallet as I don't tend to overpay for basic items and avoid the temptation to buy items at expensive convenience stores as I can immediately see (without resorting to checking online) when they don't offer competitive prices most of the time.
In addition to rough calibration it's good to know by heart some of the following:
- constants such as unit counts: seconds in a minute, minutes in a hour, hours in a day, minutes in a day (1440), etc.
- geometric formulas such as perimeters and areas of figures, volumes of solids, etc.
- units for physical quantities such speed, acceleration, force, energy, power, etc.
All those will come in handy many, many times in your whole life if you are even a tiny bit of a quantitative type (and if you're not, you should be for your own good!).
This posting is meant to show that some basic math is both fun and very useful. It's never too late to discover math for yourself, even, or maybe particularly so, if you've never really enjoyed it or had bad memories from your education (doing menial calculations instead of having fun). There are tons of math resources on the web that are easy to follow and make the learning process much more interesting. I enjoy betterexplained.com; Khan Academy is also probably very good, there are also lots of MOOCs that usually target a more specific area of math.