Exploding dice probabilities

This maths exercise was inspired by a feature called “exploding dice” in the “Chaos in the Old World” board game.

Notation

• n: number of hits
• k: number of dice
• z: number of dice with zero hits

Rules

The dice are regular six-sided dice.

The rules for rolling k (where k usually ranges from 1 to 6) dice are as follows:

1. If a 1, 2 or 3 is rolled, this die is a “miss” and is done (no more rolls).
2. If a 4 or 5 is rolled, this die is a “hit” and is done (no more rolls).
3. If a 6 is rolled, this die is a “hit” and is re-rolled, subject to the same rules (which implies it can be re-rolled multiple times if a sequence of sixes is produced). This is the so-called “exploding dice”.

Problem statement

Given those rules, figure out the probability mass function parametrized on the number of dice. Or in other words, assuming we have k dice, what is the probability of getting exactly n hits?

Chunking the problem

I only came up with a piece-wise definition of the function parametrized on n and k and for the most interesting case with n > 0 and k > 0, the formula has an internal summation so it's not a closed-form formula. Some pieces of the formula can most likely be pulled before the summation so there might exist a more succinct version that does fewer computations.

These are the three pieces which are later solved:

1. n = 0 (zero hits)
2. n > 0 and k = 0 (zero dice and more than zero hits)
3. n > 0 and k > 0 (more than zero dice and more than zero hits - the most interesting scenario)

n = 0

This is a relatively simple scenario. Each die has a probability of $\frac{1}{2}$ of getting 0 hits (by rolling 1, 2, or 3), so all k dice getting 0 hits has a total probability of $(\frac{1}{2})^k$.

To double check this result, we can think about it in a more combinatorial way and calculate the ratio of the number of ways to roll 1, 2, or 3 on k dice over all possible rolls of k dice. This should be $\frac{3^k}{6^k} = (\frac{3}{6})^k = (\frac{1}{2})^k$, so we get the same result.

n > 0 and k = 0

This probability has a constant value of 0, as you cannot get more than 0 hits with 0 dice.

n > 0 and k > 0

Single die with n hits

First, I work out the probability mass function for a single die, because it seems much more tractable than multiple dice.

Let's start with one hit, the diagram below shows how this can happen:

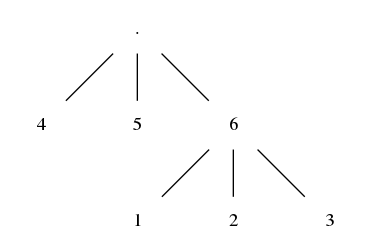
As per the graph, you can either roll a 4 or a 5 and stop, or roll a 6 followed by a 1, 2, or 3. The probability of this happening is $2 \cdot \frac{1}{6} + 3 \cdot (\frac{1}{6})^2 = \frac{5}{12}$.

For two hits, the graph has one more level:

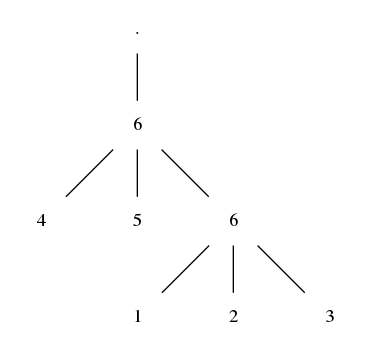
and the probability is: $2 \cdot (\frac{1}{6})^2 + 3 \cdot (\frac{1}{6})^3 = \frac{5}{72}$.

To generalize it to n hits, as per the following diagram:

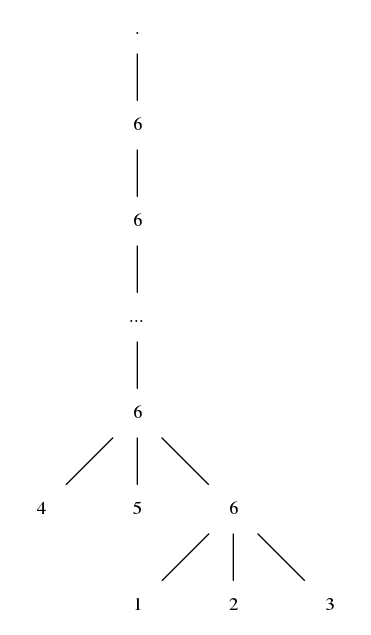
we can work out the formula to be: $2 \cdot (\frac{1}{6})^n + 3 \cdot (\frac{1}{6})^{n+1} = \frac{5}{2 \cdot 6^n}$.

Multiple dice with hits (total of n hits)

For multiple dice, we make the following observations:

1. The total number of hits (n) spread among all dice (k) is like addition of k non-negative integers (i.e. including 0) whose total is n.

   For example, if k (number of dice) = 3 and n (number of hits) = 5, here are the ways in which it can happen:

   1. 0 + 0 + 5 (3 permutations)
   2. 0 + 1 + 4 (6 permutations)
   3. 0 + 2 + 3 (6 permutations)
   4. 1 + 1 + 3 (3 permutations)
   5. 1 + 2 + 2 (3 permutations)

   Adding up all the permutations (3 + 6 + 6 + 3 + 3), we see this can happen in 21 ways. I also learnt that this number is the number of weak k-compositions of an integer and is equal to $\binom{n+k-1}{k-1} = \binom{7}{2} = 21$, which agrees with our manual calculation.

   However, counting the probabilities with weak compositions seems hard, because of the special case of dice which had 0 hits, which have different probability than non-zero-hits dice. For me, a more intuitive solution is slightly modified, namely I will be counting the number of “non-weak” compositions (where zeros are not allowed) across k minus z (z for zero-hit dice) dice and multiplying it by the product of the number of ways of distributing zeros among the remaining z dice and the probability of getting a zero.

2. The number of “non-weak” or “strict” (I don't know if these are commonly used or accepted terms) compositions is $\binom{n-1}{k-1}$ and we iterate over numbers from 0 (no dice with 0 hits) up to k-1 (only one die had any hits, n hits to be exact. Note that we cannot go all the way to k as that would imply we got 0 hits on all dice) and calculate their probabilities and then add them up.

   To exemplify, we would iterate over the following scenarios for n=5 and k=3 and z from 0 to k-1

   1. z = 0, n = 5, k = 3 (no dice had 0 hits):
      1. 1 + 1 + 3
      2. 1 + 2 + 2
   2. z = 1, n = 5, k = 2 (one die had 0 hits):
      1. 0 + 1 + 4
      2. 0 + 2 + 3
   3. z = 2, n = 5, k = 1 (two dice had 0 hits):
      1. 0 + 0 + 5

   For each of the scenarios we notice the following:

   1. Multiplying the probabilities of dice which had at least one hit, for example when k=2 and n=5 such as one die with 1 hit and the other with 4 hits, is $\frac{5^1}{2^1 \cdot 6^1} \cdot \frac{5^1}{2^1 \cdot 6^4} = \frac{5^k}{2^k6^n}$ or when k=3 and n=5 such as one die with 1 hit, the second die with 1 hit and the third die with 3 hits, is: $\frac{5^1}{2^1 \cdot 6^1} \cdot \frac{5^1}{2^1 \cdot 6^1} \cdot \frac{5^1}{2^1 \cdot 6^3} = \frac{5^k}{2^k6^n}$ which is always the same value for given k and n, i.e $\frac{5^k}{2^k6^n}$.

      So our summation is going to be:

      $\sum\limits_{z=0}^{k-1} \binom{n-1}{k-z-1}\frac{5^{k-z}}{2^{k-z}6^n}$

   2. How do we account for dice with 0 hits?

      To account for dice with 0 hits we will need the following pieces of information:

      • The probability of a die getting 0 hits (constant and equal to $\frac{1}{2}$),
      • How many 0-hit dice there were (this is given by our index variable z),
      • How many ways there are to distribute the 0-hit dice ($\binom{k}{z}$).

      So our summation now needs to absorb this information and be modified to:

      $\sum\limits_{z=0}^{k-1} \binom{n-1}{k-z-1} \frac{5^{k-z}}{2^{k-z}6^n} (\frac{1}{2})^z\binom{k}{z}$

Final definition of the function

Now that we have split/chunked the problem, we can attempt to write the definition of the probability mass function. Here is such a definition, with the domain of the function's both parameters (n and k) constrained to non-negative integers:

$$ p(n,k)= \begin{cases} \frac{1}{2^k} & \text{if } n=0\\
0 & \text{if } n>0 \text{ and } k=0\\
\sum\limits_{z=0}^{k-1}\binom{n-1}{k-z-1}\frac{5^{k-z}}{2^{k-z}6^n}(\frac{1}{2})^z\binom{k}{z} & \text{if }n>0\text{ and }k>0 \end{cases} $$